Chapter04 "데이터 요약하기"
Chapter 04-2의 주제는 '분표 요약하기' 이다.
실습전 다운로드
import gdown
import pandas as pd
# 04-1에서 만든 ns_book7 다운
gdown.download('http://bit.ly/3pK7iuu', 'ns_book7.csv', quiet = False)
# pandas로 불러오기
ns_book7 = pd.read_csv('ns_book7.csv', low_memory=False)
ns_book7.head()산점도 그리기
- 산점도: 데이터를 화면에 뿌리듯 그리는 그래프
- 두 변수 혹은 두 가지 특성 값을 직교 좌표계에 점으로 나타낸 그래프
scatter() 함수
- 산점도를 그려준다
- scatter() 함수를 호출한 다음 show() 함수 호출해 그래프 출력
- plt.scatter( x , y )
# matplotlib.pyplot 패키지 다운
import matplotlib.pyplot as plt
# x, y축이 1,2,3,4인 산점도
plt.scatter([1,2,3,4],[1,2,3,4])
plt.show
# 남산도서관 대출 데이터를 이용한 산점도
plt.scatter(ns_book7['번호'], ns_book7['대출건수'])
plt.show()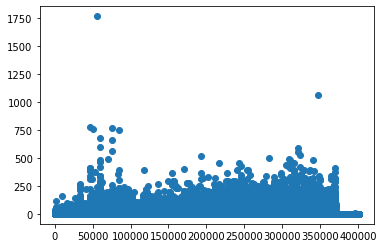
'번호' 열은 그저 일련번호이다. 그래서 딱히 특별한 의미가 없다.
'번호'에 따라 '대출건수'가 달라지는 것이 아니다. 그렇기 때문에 비교적 고르게 퍼져있다.
'대출건수' 와 '도서권수'를 비교해보겠다.
# '대출건수' 와 '도서권수'의 산점도
plt.scatter(ns_book7['도서권수'], ns_book7['대출건수'])
plt.show()
'도서권수'가 많으면 '대출건수'도 많아질까? 그런 경향을 파악하기 위해 투명도를 조절할 것이다.
투명도 조절하기
- alpha 매개변수에 0~1사이의 값으로 투명도를 조절
# 투명도를 0.1로 지정하여 산점도 나타내기
plt.scatter(ns_book7['도서권수'], ns_book7['대출건수'], alpha = 0.1)
plt.show()
0.1의 투명도에도 짙게 보이는 건 많이 겹쳐진 것. 도서권수가 적다는 것이다.
그래서 도서권수와 대출건수 사이의 관계를 파악하기 어려움
여기서 나오는 관계 : 도서권수가 많으면 대출건수가 높다(양의 상관관계), 혹은 그 반대(음의 상관관계)
- '도서권수'열 대신 '대출건수'열을 '도서권수' 열로 나눈 값을 사용
- 도서권수 당 대출건수 : x , 대출건수 : y로 산점도를 그려볼 것이다
# 도서권수 당 대출건수: average_borrows 변수
average_borrows = ns_book7['대출건수']/ns_book7['도서권수']
# scatter
plt.scatter(average_borrows, ns_book7['대출건수'], alpha = 0.1)
plt.show()
두 특성 사이에는 '양의 상관관계'가 있다고 말할 수 있다.
히스토그램 그리기
- 히스토그램: 수치형 특성의 값을 일정한 구간으로 나누어 구간 안에 포함된 데이터의 개수를 막대그래프로 그린 것
- 도수: 구간 안에 속한 데이터 개수
hist() 함수
- bins 매개변수: 구간의 개수
plt.hist([0, 3, 5, 6, 7, 7, 9, 13], bins = 5)
plt.show()
구간이 어떻게 나누어졌는지 알 수 없음.
histogram_bin_edges() 함수로 알 수 있다.
# histogram_bin_edges()
import numpy as np
np.histogram_bin_edges([0, 3, 5, 6, 7, 7, 9, 13], bins = 5)
# 결과
# array([ 0. , 2.6, 5.2, 7.8, 10.4, 13. ])각각 구간의 시작 지점(이상)을 보여준다. 2.6은 두 번째 구간으로 간다.
- 가상의 데이터로 히스토그램 제작: randn() 로 난수 생성
# seed() 함수로 유사난수 생성
np.random.seed(42)
random_samples = np.random.randn(1000)
# random_samples가 표준정규분포를 따르는지 확인
print(np.mean(random_samples), np.std(random_samples))
# 결과
# 0.01933205582232549 0.9787262077473543평균이 0에 가깝고, 표준편차가 1에 가까울수록 표준정규분포를 따른다.
# histogram
plt.hist(random_samples)
plt.show()

- 남산도서관 대출 데이터에서 '대출건수' 히스토그램 그리기
# 남산도서관 대출 데이터에서 '대출건수'
plt.hist(ns_book7['대출건수'])
plt.show()
대출건수는 작다.
첫 번째 구간의 도서가 너무 커서 다른 구간에 도수값이 생기지 않았다.
구간 조정하기
- 한 구간의 값이 너무 커서 다른 구간에 도수값이 생기지 않음
- y축을 로그 스케일로 바꿈: yscale() 함수에 log 지정
- 로그 스케일: 로그 함수 적용
- matplotlib은 기본적으로 밑이 10인 로그 함수 사용
# yscale() 함수
plt.hist(ns_book7['대출건수'])
plt.yscale('log')
plt.show()
# x축 구간 더 세세하기 보기
plt.hist(ns_book7['대출건수'], bins = 100)
plt.yscale('log')
plt.show()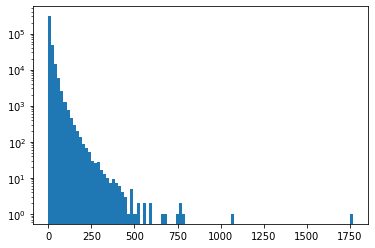
- 도서명 길이는 정규분포에 가까울까?
- apply메서드로 len 함수 적용한 title_len변수는 판다스 시리즈 객체
# 도서명 길이는 정규분포에 가까울까?
title_len = ns_book7['도서명'].apply(len)
plt.hist(title_len, bins = 100)
plt.show()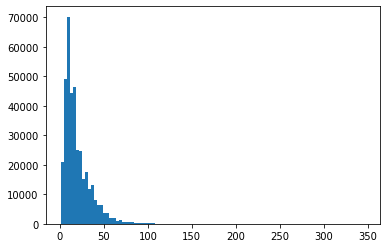
# xscale로 왼쪽으로 편중된 데이터가 골고루 그려지게 하기
plt.hist(title_len, bins = 100)
plt.xscale('log')
plt.show()
상자 수염 그림 그리기
- 상자 수염 그림: 최솟값, 세 개의 사분위수, 최댓값 이렇게 다섯 개의 숫자를 사용해 데이터를 요약하는 그래프
- 사분위수 계산: 25%와 75%지점을 밑면과 윗면으로 하는 직사각형
- 중간값, 즉 50%에 해당하는 지점에 수평선 긋기
- 밑면과 윗면에서 사각형의 높이의 1.5배만큼 떨어진 거리안에서 가장 멀리있는 샘플까지 수직선 긋기
- 최솟값과 최댓값까지 데이터를 점으로 표시 = 이상치
boxplot() 함수
plt.boxplot([ns_book7['대출건수'],ns_book7['도서권수']])
plt.show()
# y 스케일
plt.boxplot([ns_book7['대출건수'],ns_book7['도서권수']])
plt.yscale('log')
plt.show()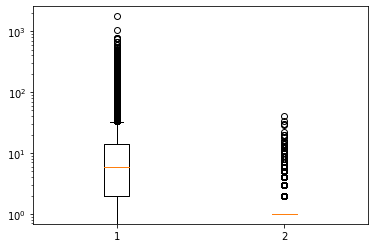
상자 수염 그림 수평으로 그리기
- vert 매개변수: True -> False로 조정
- 로그 스케일도 바뀜: y -> x
# 축 바꾸기
plt.boxplot([ns_book7['대출건수'],ns_book7['도서권수']], vert = False)
plt.xscale('log')
plt.show()
수염 길이 조정하기
- 기본적으로 IQR의 1.5배(1,3의 차)
- boxplot() 함수의 whis 매개변수
# 수염 길이 조정
plt.boxplot([ns_book7['대출건수'],ns_book7['도서권수']], whis = 10)
plt.yscale('log')
plt.show()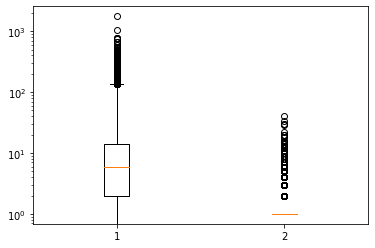
# 백분율로 지정
plt.boxplot([ns_book7['대출건수'],ns_book7['도서권수']], whis = (0,100))
plt.yscale('log')
plt.show()
기본미션

실습코드
https://colab.research.google.com/drive/1M6abnAlxB9s4YDnyMvU-a6wrqmOcwyOS?usp=sharing
'Data Analysis > 혼공학습단9기' 카테고리의 다른 글
| 혼자 공부하는 데이터 분석 with 파이썬: 5주차(Chapter 05-2) (0) | 2023.02.19 |
|---|---|
| 혼자 공부하는 데이터 분석 with 파이썬: 5주차(Chapter 05-1) (0) | 2023.02.19 |
| 혼자 공부하는 데이터 분석 with 파이썬: 4주차(Chapter 04-1) (0) | 2023.02.19 |
| 혼자 공부하는 데이터 분석 with 파이썬: 3주차(Chapter 03-2) (0) | 2023.01.26 |
| 혼자 공부하는 데이터 분석 with 파이썬: 3주차(Chapter 03-1) (0) | 2023.01.25 |



